Tous les Yards ne sont pas égaux

Introduction aux EP et EPA

Le 29 Septembre 2019 les Texans affrontent les Panthers. Sur leur première série, les joueurs de Houston se retrouvent en 3ème tentative et 1 yards à parcourir. Carlos Hyde prend le ballon, parcourt 3 yards avant de se faire plaquer par Luke Kuechly. Plus tard dans la même mi-temps, les Panthers font aussi face à une troisième tentative mais il y a cette fois ci 14 yards à parcourir. McCaffrey hérite du ballon et arrive à gagner 13 yards avant que Justin Reid mette fin à sa course. On peut se demander quelle est la meilleure course entre les deux ?

Si on se fie aux statistiques souvent diffusées par les médias traditionnels, le run de McCaffrey est bien meilleur, il a gagné 4 fois plus de yards sur cette course que Hyde en a gagné sur la sienne. Mais est ce bien vrai ? Le run de McCaffrey a beau avoir fait gagner 13 yards il a mis fin à la série, il n’a pas permis d’obtenir le first down. De plus si il a pu parcourir 13 yards c’est en partie grâce à la défense des Texans qui ne s’attendait pas une course. En revanche la course de Hyde a permis, elle, d’obtenir un first down ce qui permet de continuer le drive et d’avoir une plus grande chance d’obtenir des points. Sur cet exemple cela nous semble absurde de considérer qu’une course est meilleure que l’autre juste sur le nombre de yards… et bien c’est pourtant ce qu’il se passe régulièrement quand on lit des comparaisons de joueurs basés sur leur total de yards (si on a de la chance on nous donne le volume pour avoir un semblant de contexte). Tous les yards ne sont pas les mêmes, et c’est de ce postulat que commence la création des Expected Points.

Mais c’est quoi exactement les Expected Points ?

Pour une situation donnée précédent un play, les EP donnent la probabilité du prochain événement. Les 7 événements possibles sont:

• Touchdown (7 points)
• Field Goal (3 points)
• Safety de l’adversaire (2 points)
• Aucun point (0)
• Safety (-2 points)
• Field Goal de l’adversaire (-3 points)
• Touchdown de l’adversaire (-7 points)

Le calcul des Expected Points se fait donc comme ceci :

EP = 7*P(TD) + 3*P(FG )+2*P(OppSafety) + 0*P(Aucun Point) – 7*P(Opp.TD) – 3* P(Opp.FG) – 2 P(Safety)

(P(TD) est la probabilité de marquer un TD sur le play suivant et P(Opp.TD) la probabilité que ce soit l’adversaire qui en marque un)

La question est donc: comment sont calculées ces probabilités ? Et bien grâce aux centaines de milliers de play qui ont eu lieu précédemment en NFL. Grossièrement, si une équipe est en 2nd&5 sur ses 35 yards, on regarde toutes les situations similaires qui ont eu lieu lors des 10 dernières années, et on regarde combien de fois le play d’après a abouti sur un TD, un FG etc… C’est une façon très simplifiée de voir les choses mais qui résume bien le principe de cette statistique.

Il s’agit plus précisément d’un modèle de régression logistique multinomial générant des probabilités pour les sept types possibles d’événements qui peuvent arriver durant la mi-temps. Plus la valeur des EP est grande plus la probabilité de marquer des points est importante pour l’équipe qui a la balle.

La plupart des modèles de calcul d’EP se basent sur un plus de facteurs que l’exemple que j’ai pris plus haut. On retrouve généralement:

• La distance à l’en-but adverse
• Le down
• Le nombre de yards à parcourir pour obtenir un first down
• Un indicateur pour savoir si on est en 2 minutes warning ou non

Mais le modèle pondère aussi chaque donnée par le différentiel au tableau d’affichage. En effet il n’est pas rare que des équipes qui mènent largement au score se relâchent et permettent à l’équipe adverse de marquer quelques points qui n’ont finalement aucune valeur. Plus une équipe est loin au tableau d’affichage moins ce qu’elle va faire aura une valeur ajoutée sur l’aboutissement du match.

Je vous mets ci dessous la valeur des EP pour les différents down en fonction de la zone du terrain où l’on se situe. Les graphes proviennent d’un article de Ron Yurko un des plus grand contributeurs à la démocratisation de cette statistique. Je vous invite à lire ses travaux pour ceux qui voudraient plus de détail: https://www.cmusportsanalytics.com/nfl-expected-points-nflscrapr-part-1-introduction-expected-points/

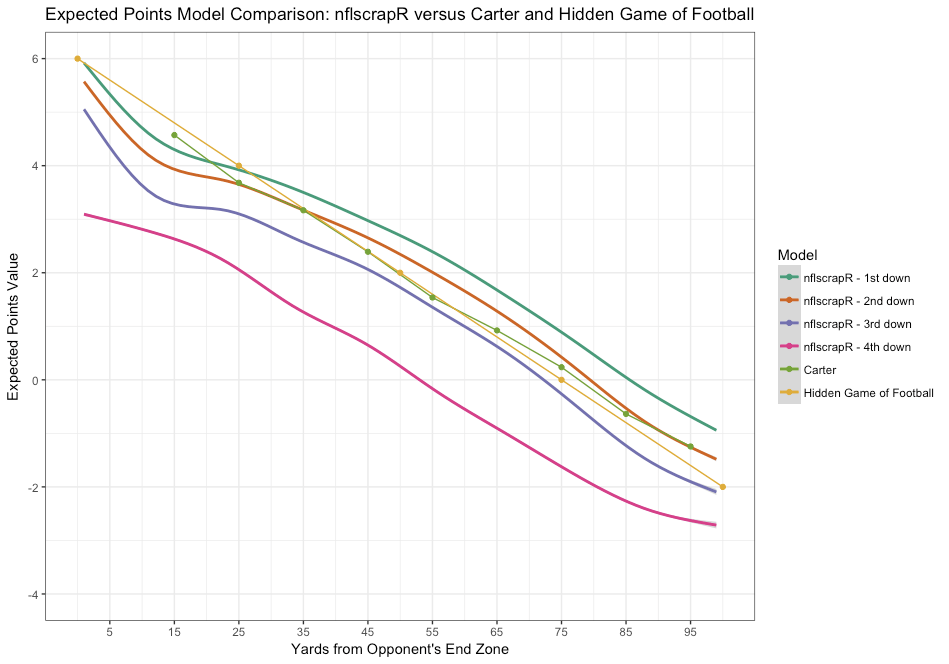
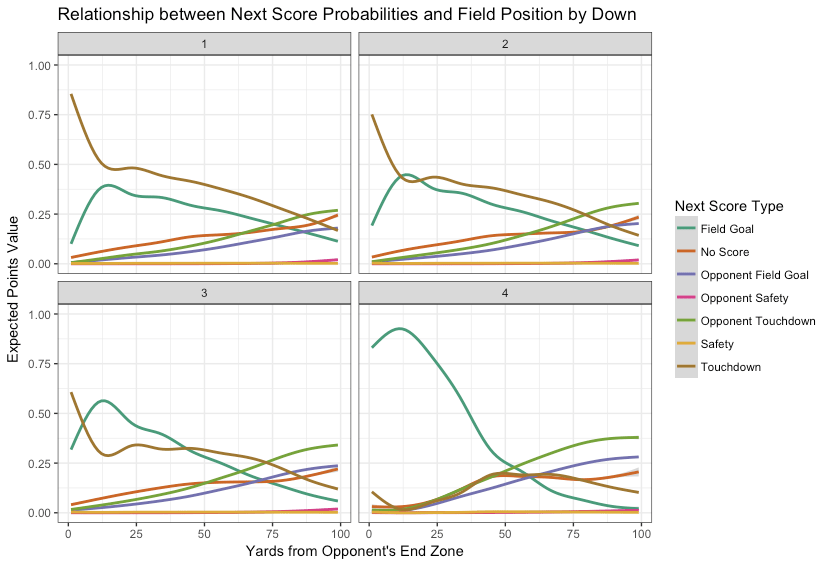
Sur les graphes ci dessus on voit par exemple que si l’on est en 4ème down près de l’en-but adverse, la probabilité de marquer un field goal est très élevée, parce que les équipes optent en général pour un coup de pied dans cette situation.

Mais quel rapport avec la valeur et l’efficacité d’un joueur ? Et bien c’est ce que nous allons voir avec les EPA (Expected Points Added)

Comprendre les Expected Points Added

Maintenant que l’on a défini les EP, le calcul des EPA est en fait très simple. Imaginons que nous sommes en 1st Down & 10 sur nos 25 yards. Comme nous l’avons vu dans la première partie, cette situation a une valeur d’EP qui lui est propre (Appelons la EP(1) ). Sur ce premier Down notre quarterback va compléter une passe de 5 yards nous amenant donc en 2nd Down & 5 sur nos 30. Cette situation a elle aussi une valeur d’EP attitrée ( EP(2) ). Et bien la valeur en EPA de ce jeu est simplement la différence d’ EP entre les deux situations.

EPA = EP(1) – EP(2)

Ainsi on sait vraiment ce que vaut cette passe. Plus la valeur d’EPA d’un play est grande plus ce play donne de chance d’aller marquer des points. On peut donc pour un joueur donné, regarder à combien d’EPA il a contribué durant le match (en les additionnant) et diviser le total par son nombre de play. On a ainsi une vraie valeur de l’efficacité d’un joueur qui ne prend pas en compte les yards et situations superflues.

Si l’on reprend notre exemple du début, la course de Hyde vaut 0,08 EPA alors que celle de McCaffrey -0,1 ( la valeur est négative car dans cette situation, en n’obtenant pas le first down, c’est l’adversaire qui a le plus de chance de de marquer les prochains points). Une répartition bien plus juste que celle donnée par le nombre de yards.

Limites du modèles

La principale limite est que le modèle ne prend pas en compte les joueurs présents sur la pelouse (chose impossible à faire avec les bases de données accessibles), à priori la probabilité de scorer peut varier avec la qualités des joueurs sur le terrain.

De plus comme toute statistique elle n’est pas absolue, si on l’utilise pour quantifier l’efficacité d’un QB par exemple, elle ne donne en aucun cas l’impact du système, le niveau de la ligne offensive etc… Il faut avoir une idée de ce qu’elle représente quand on l’utilise (c’est valable pour toutes les statistiques).

Conclusion

Avec cette statistique on peut donc avoir une vraie idée de ce qu’apportent les joueurs sur le terrain, en prenant en compte: le contexte de la possession, la différence au tableau d’affichage etc… Ces données sont obtenues sans se baser sur des statistiques fallacieuses comme le nombre total de yards ou de TD qui ne veulent finalement pas dire grand chose. Et ça, c’est une bonne nouvelle.